3.7.1节中第7行讲轨迹文件trajectory.txt中的数据“均是以世界坐标系到机器人坐标系记录”，这个弄错了吧，根据后面的程序代码，应该是“均是以机器人左边系到世界坐标系记录”，因为程序中直接将机器人坐标系中的向量左乘变换矩阵变换到世界坐标系，而变换矩阵是直接用txt文件中的四元数生成的，并没有求其逆矩阵。
四元数没有求逆的情况下，相当于坐标变换已经求逆。你如果仍然有疑惑，可以参考我的博客，我自己也被这件事折腾了半天：https://mp.csdn.net/mp_blog/creation/editor/140700853
赞
请问畸变多项式是如何推导出来的呢？我现在只知道这个公式是通过四种常用鱼眼模型再通过泰勒展开统一得到的，那么第二版书中101页公式5.10是如何得到的呢，这幅图片是四种模型之一。求大佬们指点一二
不是这么推导的。泰勒公式是个万金油公式，可以适配任何函数曲线。展开项数越多表示越精细而已
就是泰勒级数展开，但注意到不能包含奇数项
有人第三章可视化运行出来了吗，请教以下
我想问下第七章运行3D到2D代码的时候，如果是自己的图像，深度图怎么获得
3.7.1节中第7行讲轨迹文件trajectory.txt中的数据“均是以世界坐标系到机器人坐标系记录”，这个弄错了吧，根据后面的程序代码，应该是“均是以机器人左边系到世界坐标系记录”，因为程序中直接将机器人坐标系中的向量左乘变换矩阵变换到世界坐标系，而变换矩阵是直接用txt文件中的四元数生成的，并没有求其逆矩阵。
赞
请问畸变多项式是如何推导出来的呢？我现在只知道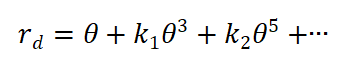
这个公式是通过四种常用鱼眼模型再通过泰勒展开统一得到的，那么第二版书中101页公式5.10是如何得到的呢
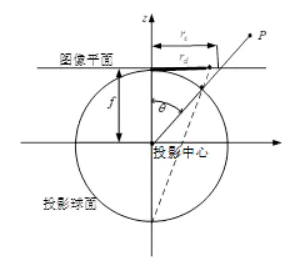，这幅图片是四种模型之一。求大佬们指点一二
有人第三章可视化运行出来了吗，请教以下
我想问下第七章运行3D到2D代码的时候，如果是自己的图像，深度图怎么获得