高博您好,第六章中,式6.41中的增量方程,相比于式6.32/6.33中的增量方程,等式两边增加了误差方差的倒数。
罗德里格斯公式(3.15)在n=[1,0,0]^T的情况下,R应该收敛于基本坐标变换矩阵然而,实际计算表明二者差一个转置或求逆,即图中的sin\alpha前面的符号都反了,这是什么原因呢?
我已经解决了这个问题并写成博客。有兴趣的朋友可以去看我的博客:https://mp.csdn.net/mp_blog/creation/editor/140700853
@zealot@xm 大佬,您发的这个博客网址有点问题,除了您自己的账号我们无法查看
167页,书上说:x1,x2是两个像素点的归一化平面上的坐标,感觉这里说的不对,根据上面给出的公式,x1,x2应该是空间点P在两个坐标系下的归一化平面坐标
第二版84页注2是否有误,好像不是只能求行向量关于列向量的导数,这里只是布局不同,不知道是否正确这种想法,请教一下
高博您好,第六章中,式6.41中的增量方程,相比于式6.32/6.33中的增量方程,等式两边增加了误差方差的倒数。
罗德里格斯公式(3.15)在n=[1,0,0]^T的情况下,R应该收敛于基本坐标变换矩阵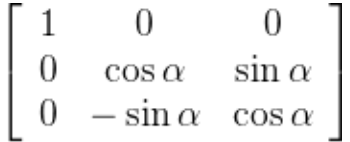
然而,实际计算表明二者差一个转置或求逆,即图中的sin\alpha前面的符号都反了,这是什么原因呢?
167页,书上说:x1,x2是两个像素点的归一化平面上的坐标,感觉这里说的不对,根据上面给出的公式,x1,x2应该是空间点P在两个坐标系下的归一化平面坐标
第二版84页注2是否有误,好像不是只能求行向量关于列向量的导数,这里只是布局不同,不知道是否正确这种想法,请教一下